Online articles, commentaries, papers
Navigation links at the bottom of the page
The mathematics of maintenance

This explanation of the mathematics applicable to equipment maintenance will interest anyone employed in the maintenance of large electro-mechanical installations. The principles here discussed (with the sample study of a nuclear generating station), can with advantage be applied to any large plant and equipmen. That includes oil refineries, off-shore drilling rigs, petro-chemical installations, hospitals, airports, manufacturing plants and ocean-goiong vessels.

The original paper from which this account of maintenance mathematics was adapted was written and presented at the 16th Inter-RAM Conference of Power Generation and Transmission Utilities at Monterey, CA.,1986. It was published in the proceedings of the conference and later appeared in the Power Engineering Journal, December 1989.

The work of I. Walker, former superintendent of quality assurance of Ontario Hydro, in developing the probability analysis of equipment and co-author of the original paper read at the 16th Inter-RAM conference is fully acknowledged.

All the costs quoted in this article are expressed in Canadian dollars. In fact, as will be recognized, the actual figures quoted have little bearing on the methods and principles, for those values are relative values only.

This article discusses RAM analysis (RAM meaning reliability, availability and maintainability), Poisson distribution, and offers a solution to the balance of maintenance load and capacity. As an introduction to aspects of equipment maintenance mathematics, the load-capacity equation for computerized management is discussed first.

Organizing and maintaining large electro-mechanical equipment is a major undertaking. It requires managers to control the work, trades people to do it, subcontractors for specialized services not available in-house, purchasing agents for a spare parts and material programme, storage and distribution management. This all adds up to many hours of work, which is an element of the mathematical equation. All in all, the total hours required to maintain a given installation is represented by the letter L while the total capacity of the organization in work hours to meet that load is expressed as C.

That is, ideally, the maintenance load in L hours must equal the maintenance work capacity in C hours for the highest efficiency to be achieved; i.e. L = C.

The equation is true only when the total maintenance load in work hours is balanced by the available capacity in work hours. Both L and C, however, are variables and cannot be otherwise. That is, L is variable because equipment breakdown cannot with accuracy be predicted; C is variable because those who perform the work are available or not available when needed for a variety of reasons. Nevertheless, the L = C statement provides a platform on which to develop a programmable computerized system.

Maintenance Load L: The total load in any installation is the sum of three components, which are:

1. Periodic maintenance, which consists of measurable scheduled tasks that are expressed by the term Rm.

2. Predictive maintenance, which involves tasks that, within limits, can be scheduled to suit equipment outages. Tasks in this category are represented by the term Pm.

3. Breakdown maintenance, which is work either of immediate concern, or in a short-term planning category, expressed as Bm.

That is, L = Rm + Pm + Bm

Maintenance capacity C: The capacity (C) of the enterprise to meet the total maintenance load (L) is, as earlier stated, variable, but can be calculated using several elements. That is:

1. The total available 'standard' hours of the maintenance staff involving all trades has labour productivity in the range of 50% to 60%, expressed in the term symbol Sh.

2. Next are the available additional hours obtainable through overtime (of selected trades), for which the term Oh is used.

3. Lastly, the maintenance capacity available are those hours external to the 'on-staff' maintenance force (by sub-contract, for example), for which the term Ch is used.

Therefore, the total available capacity C = Sh + Oh + Ch or

as L = C

Rm + Pm + Bm = Sh + Oh + Ch

In each of the elements Rm, Pm and Bm a further breakdown of hours required is possible and defined. For example, in known periodic or regular maintenance tasks (Rm) the required mix of hours by trades is available from existing hard copy or electronic records. For given periodic maintenance on a valve, say, a crew of two fitters and one electrician (for control and signaling connections) might require an elapsed time of eight hours. That is, the work comprises two electrical hours (one to disconnect, another to connect and test) and two fitters for six hours. In other words, within the limits defined, the elapsed time in hours required by the Rm load is fixed. In the case of the example Rm = 8 hours.

The available standard hours (Sh) in this instance are E electrical hours 2, and F fitter hours or 2 x 6 = 12 hours. Hence Rm = Sh = 2E + 12F = 14 work hours to be satisfied.

To measure the capacity of the system, each element of the available capacity in work hours by trades must be plotted into the programme: welders, fitters, electricians, control and computer system technologists, machinists, carpenters and the entire range of specialist trades that make up a given maintenance work force. The same applies to the available overtime hours for each trade and the subcontract and specialist hours that are available.

By developing a programme of maintenance work by trades and elapsed hours required, and measuring or estimating the available hours to meet the work load, using the principles here outlined, a sensible and workable maintenance equation can be programmed. Such programs can be, and have been, implemented.

Balancing load and capacity is but one technique used to minimize the total maintenance load.

This in turn reduces the maintenance cost. Figure 1 shows the expected trend in direct maintenance cost that can result from an effective program. By changing from unplanned maintenance (related to equipment failure - see below) to a 70% preventive maintenance element, the cost saving in a Canadian nuclear generating station was 30% of the original estimated cost.

By increasing the preventive maintenance component from the 30% level in 1986 to 70% by 1990, the estimated reduction in cost was 15% or $2.3m a year. This was a net saving. Furthermore, there was no evidence of a reduction in production reliability. 		Figure 1,
Expected trend

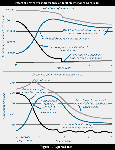This in turn reduces the maintenance cost. Figure 1 shows the expected trend in direct maintenance cost that can result from an effective program. By changing from unplanned maintenance (related to equipment failure - see below) to a 70% preventive maintenance element, the cost saving in a Canadian nuclear generating station was 30% of the original estimated cost.

By increasing the preventive maintenance component from the 30% level in 1986 to 70% by 1990, the estimated reduction in cost was 15% or $2.3m a year. This was a net saving. Furthermore, there was no evidence of a reduction in production reliability.

A computerized maintenance system of the type described is one way to raise efficiency of the overall maintenance program. A parallel program that works well is an analytical system that is known as the RAM technique, where RAM is an abbreviation of reliability, availability and maintainability. The RAM method of analysis was used at a Canadian nuclear generating station to improve maintenance practices on specific types of equipment. They were applied to:

a. improve a vibration monitoring program for rotating equipment;
b. for the inspection and cleaning of heat exchangers; and
c. to institute a comprehensive valve maintenance program.

RAM analysis was part of a reliability-centred approach to improve the overall maintenance program. If it worked successfully on selected systems and equipment it could be applied to any high-cost installation. The effectiveness of the method was reflected in generating unit availability, maintenance cost, and unit energy costs. RAM analysis is also a form of probability examination as used in the example that follows. To conduct this analysis and apply it to a moderator cooling system, specific steps were described, steps that might also be regarded as objectives on which to base the analysis. These were to:

1. identify the equipment that causes 80% of (in the case of the nuclear generating station) the generating unit incapability;

2. categorize the 18% of equipment that consumes 62% of the overall maintenance costs;

3. analyze the maintenance experience over the past three years;

4. use RAM techniques such as failure modes and effects analysis (FMEA) and 'goal trees' to identify failure modes and reliability requirements;

5. use probability risk assessment (PRA) to analyze the consequences of critical failure modes that impair system reliability;

6. develop a maintenance strategy to reduce the frequency of critical failure modes or, at least, to lessen their consequences;

7. compare benefits in relation to the costs of the proposed strategy and implement those options that are the most cost-effective; and

8. regularly review and monitor the program

Moderator cooling system

Figure 2 is a diagrammatic representation of a moderator cooling system used for the analysis. In addition to the calandria, it shows various items of equipment - pumps, heat exchanger and valves - that make-up the cooling system. This removes about 150 Mega watts (MW) of waste heat from the reactor at low pressure and temperature. The moderator is heavy water.

Immediately following Figure 2 is a 'truth table', which lists each component and its state. That is, it specifies the possible failure modes for the loop.

Experience over a three-year period was reviewed to compare preventive and corrective maintenance with the historical failure record. Significant failures occurred in pump bearings and seals and as tube leaks in the heat exchanger. A significant failure is a major one requiring immediate attention.

Bearings were replaced on the spare pump with the unit on load. Seal replacement required a unit outage of 132 hours. This time was needed to drain the moderator system to isolate the pump due to internal leakage through the seats of the pump isolating valves, in three cases out of four. To locate and plug a leaking tube, the exchanger must first be isolated. This operation requires a unit de-rating to 50% capacity for at least ten days.

The critical failures in this study, therefore, were pump seals and tube leaks. The historical failure rates are two seal failures per year out of a population of eight pumps, and one tube failure in 10 years from a population of eight heat exchangers.

The failure probabilities are derived, assuming a Poisson distribution of failure (a Poisson distribution is a probability distribution whose mean and variance have a common value k and whose frequency is f(x) = kxe-k/x!, for x = 0,1,2,...) The probability of failure during the time interval from 0 to t is exponential. Based on this equation, the failure possibilities are pump seal 0.865 and heat exchanger tubes 0.095. The probability of a dual seal failure on one pump is (2/8)2 = 0.063.
   
Figure 2. Moderator cooling system Table 1. Truth table Figure 3. Goal tree prevention of moderator cooling loss
Pump Seal Failure

Seal failure is closely related to bearing wear. Displacement of the pump shaft, caused by excessive bearing wear, results in rapid deterioration of the carbon seal faces. Bearing wear can be monitored by transducers mounted on the bearing housing. Vibration limits are set to make sure that the shaft displacement does not exceed the allowable tolerance on the seal.

Seal failures are reduced at the additional expense of a vibration monitoring installation and the cost of the data collection needed to measure deterioration of the bearing. The net electrical rating per generating unit is 769 MW. The replacement energy cost for the unit in question was (at the time of the study) $16/MWh. Therefore, the probable annual production loss due to seal failures is 0.063 x 132 x 769 x 16 x 0.75/1000 = $76,000/yr.
Table 2. Benefit/cost analysis

The probable reduction in dual seal failures due to vibration monitoring is conservatively assessed at 50%. It follows, therefore, that the probable production improvement is $38,500/yr. (see Table 2).

The cost of installing, operating and maintaining the vibration monitoring system is an estimated $840/yr. Hence, vibration monitoring is clearly a cost-effective option.
Note: The cost estimates stated throughout this analysis are, of course, relative. That is, for purposes of illustrating the analytical method of maintenance, the values stated are relative and apply regardless of the currency or for that matter the type of equipment considered.
Heat exchanger tube failures

The preferred way to prevent tube failures is to inspect the lead heat exchanger during the planned shutdown every four years. Eddy current equipment is used to inspect 10% of the tubes. The estimated cost of inspection is $10 K. The annual inspection cost is therefore $2,500. The probably production loss resulting from tube failures is

0.095 x 10 x 24 x 760 x 0.5 x 16/1000 = $140,300/yr

Tube inspection, therefore, is a valuable economy.

In summary, the additional cost of prevention production losses amounting to $217,000/yr from dual pump seal and tube failures is $3,300/yr. The benefit-to-cost ratio at 66:1 is high.

Table 3. Ranking by system of production loss
and maintenance cost

Production losses caused by equipment failure and the direct maintenance cost for station systems used in this study were obtained from corporate data bases. Rankings for the preceding five-year period are given in Table 3. It is obvious from this tabulation that, considering the cost savings to be achieved, the priorities of equipment maintenance need to be revised.

At the end of the study period, the de-rating adjusted forced outage rate for the generating station was 9.4%. This was the equivalent production loss due to equipment failure and human factors combined. The loss resulting from equipment failure is estimated at 8%. The replacement energy cost was:

769 x 4 x 365 x 24.5 x 16 x 0.08/1,000,000 = $34.5M/yr

A 20% reduction in production loss is achievable by improving maintenance effectives on selected equipment. Based on experience, it is a reasonable assumption that 60% of the loss is caused by 20% of the equipment. Hence, the probable improvement to production by means of improved maintenance with respect to reliability on selected equipment is:

34.5 x 0.2 x 0.8 = 5.5M/yr

Assuming a conservative benefit-to-cost ratio of 2:1, the net saving from improved production is $2.8M/yr.
Conclusion
As noted throughout this article, the principles discussed are applicable to any large installation regardless of its type, function or complexity. The same RAM techniques that have been applied by way of example to a system in a nuclear power generating station would work equally as well for an off-shore oil-drilling platform, an ocean-going vessel or major manufacturing plant. The application of the principles discussed are limitless.
Bibliography & references:

The Mathematics of Maintenance, A. W. Cockerill, Delta Tech Systems, and I. Walker, Ontario Hydro, 16th Inter-RAM Conference, Monterey, Ca., 1989.

Organization and Management of a Preventive Maintenance Program, seminar, B. M. Coulter, Emerson Consultants, Toronto, 1987.

Bruce NGS 'A' Maintenance Review Program, CNS-IR-01550-1, 1986, A. B. Powell.
RAM Applications in Power Generation, Tutorial I, 14th Inter-RAM Conference, Toronto, 1987.

Selection of Optimum Inspection Frequency to Prevent First In-Service Failure, CNS-IR04162-2, E.W. Thurygill, 1984.

Development of a Maintenance Program, I. Walker, ANS International Meeting on NPP Operation, Chicago, 1987.

A Production Control System, A. W. Cockerill, The Canadian Manager Journal, 1971.

Vibration Monitoring Program Assessment, BGS-INF-0151O-1, G. Baggs, 1987.

Pickering NGS Maintenance Allocation System, P. F. Tremblay, 1987.

Original paper published in
Proceedings of the 16th Inter-RAM Conference
 
BACK NEXT
 
Delta Tech Systems Inc
HOME PAGE
Duke of York's Royal Military School
Royal Hibernian Military School
Reminiscences of a Queen's Army  Schoolmistress
World War I - The war to end all wars
Books and Militaria 		Publications and Papers
Wellington on Waterloo
Correspondence
Related Links
Contact

© A. W. Cockerill 2005

Site Map     Contact me